​什么是共识算法 背景 分布式系统集群设计中面临着一个不可回避的问题，一致性问题 对于系统中的多个服务节点，给定一系列操作，如何试图使全局对局部处理结果达成某种程度的一致？ 这个一致性问题大致有如下的场景： 节点之间通讯不可靠的，延迟和阻塞 节点的处理可能是错误的，甚至节点自身随时可能宕机 节点作恶 举例说明，就比如有两家电影院同时售卖总量一定的电影票，在这样的场景下，要如何设计方式来保证两家电影院协调同步不出现超卖或者错卖的问题呢？ 共识算法，就是解决对某一提案（目标，投票等各种协作工作），大家达成一致意见的过程 比如上述的买票问题，就可以有如下的设计： 1.每次卖票打电话给其他电影院，确认当前票数 2.协商售卖时间，比如一三五A卖，二四六B卖 3.成立个第三方存票机构，它统一发票 通过以上的设计，可以看出一个很重要的解决一致性算法的解决思路，即： 将可能引发不一致的并行操作进行串行化，就是现在计算机系统里处理分布式一致性问题基础思路和唯一秘诀 著名的共识设计理论 FLP 不可能性原理 共识算法的理论下限 提出该定理的论文是由 Fischer, Lynch 和 Patterson 三位作者于 1985 年发表，该论文后来获得了 Dijkstra（就是发明最短路径算法的那位）奖。 FLP原理认为对于允许节点失效情况下，纯粹异步系统无法确保一致性在有限时间内完成。 三人三房间投票例子 三个人在不同房间，进行投票（投票结果是 0 或者 1）。三个人彼此可以通过电话进行沟通，但经常会有人时不时地睡着。比如某个时候，A 投票 0，B 投票 1，C 收到了两人的投票，然后 C 睡着了。A 和 B 则永远无法在有限时间内获知最终的结果。如果可以重新投票，则类似情形每次在取得结果前发生 带入到计算机领域就是说，即便在网络通信可靠情况下，一个可扩展的分布式系统的共识问题的下限是无解。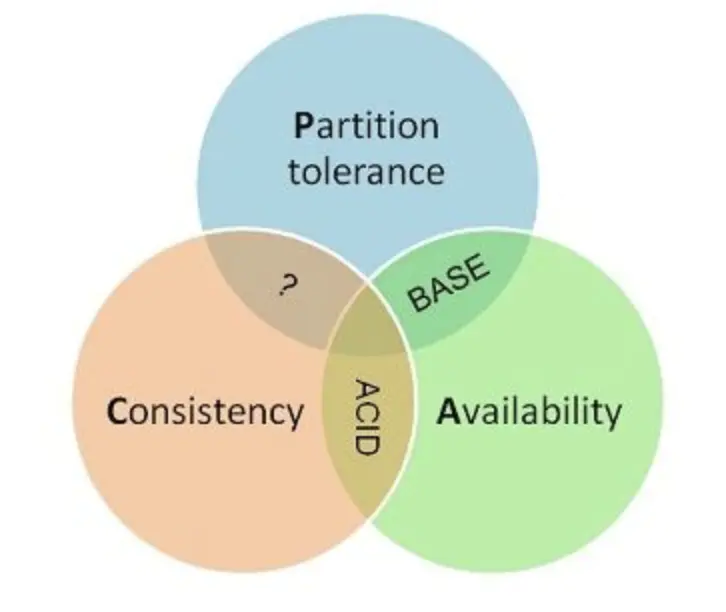即可靠性的下限是0% CAP 分布式系统领域的重要原理 CAP 原理最早由 Eric Brewer 在 2000 年，ACM 组织的一个研讨会上提出猜想，后来 Lynch 等人进行了证明 • C（一致性）：所有的节点上的数据时刻保持同步，即数据一致 • A（可用性）：每个请求都能在一定时间内接受到一个响应，即低延迟 • P（分区容错）：当系统发生分区时仍然可以运行的 定理：任何分布式系统只可同时满足二点，没法三者兼顾。即数据一致，响应及时，可分区执行不可能同时满足。 举个例子： 一个分布式网路上，某一个节点有一组依赖数据A，当网络无延迟，无阻塞时，依赖于X的操作可正常进行。但网络无延迟阻塞在现实世界中是没法100%保证的，那么当网络异常时，必然会产生分布式系统的分区和孤岛，那当一个执行操作在A分区之外时，如果要保证P,即当系统发生分区时仍可运行，就需要在分布式系统中多个节点有X的备份数据，以应对分区情况。则这时候就需要在C,A之间做出选择。 假如选择C，即要保证数据在分布式网络中的一致性，那么就需要在X每次改动时，需要将全网节点的X数据同步刷新成最新的状态，那么在等待数据刷新完成之前，分布式系统是不可响应X的依赖操作的，即A的功能缺失 假如选择A，即要突出低延迟的实时响应。那么在响应的时候，可能全节点的X数据并没有同步到最新的状态，则会导致C的缺失。 上面看上去有些绕，那么你只要记住这句话， CAP原理在分布式网络系统的应用讨论，其实就是讨论在允许网络发生故障的系统中，该选择一致性还是可靠性？ 如果系统重视一致性，那么可以基于ACID原则做系统设计 即 Atomicity（原子性）、Consistency（一致性）、Isolation（隔离性）、Durability（持久性）。 ACID 原则描述了对分布式数据库的一致性需求，同时付出了可用性的代价。 • Atomicity：每次操作是原子的，要么成功，要么不执行； • Consistency：数据库的状态是一致的，无中间状态； • Isolation：各种操作彼此互相不影响； • Durability：状态的改变是持久的，不会失效 相应的有一个BASE原则，（Basic Availiability，Soft state，Eventually Consistency）则强调了可用性。 经典的共识算法设计 业内，针对节点异常的情况，会有两种分类 1.故障的，不响应的节点，成为非拜占庭错误 2.恶意响应的节点，称为非拜占庭错误 Paxos 最早的共识算法 非拜占庭算法的代表 Paxos有三种角色： • proposer：提出一个提案，等待大家批准为结案。客户端担任该角色； • acceptor：负责对提案进行投票。往往是服务端担任该角色； • learner：被告知结案结果，并与之统一，不参与投票过程。即普通节点 系统运行由proposer驱动，当合法提案在一定时间内收到1/2以上投票后达成共识。 因此，可得出无法达成共识的条件： 1.proposer故障 2.二分之一以上acceptor故障 拜占庭问题与BFT(Byzantine Fault Tolerant) 算法 Leslie Lamport 1982 年提出用来解释一致性问题的一个虚构模型。 拜占庭是古代东罗马帝国的首都，由于地域宽广，守卫边境的多个将军（系统中的多个节点）需要通过信使来传递消息，达成某些一致的决定。但由于将军中可能存在叛徒（系统中节点出错），这些叛徒将努力向不同的将军发送不同的消息，试图会干扰一致性的达成。 拜占庭问题即为在此情况下，如何让忠诚的将军们能达成行动的一致。 对于拜占庭问题来说，假如将军总数为 N，叛变将军数为 F，则当N>=3F+1时，问题才有解，即叛变的将军不超过1/3时，存在有效的算法，如BFT，不论叛变者如何折腾，忠诚的将军们总能达成一致的结果。 这是一个数学论证的结论，有兴趣的同学可以自行推导。 PBFT 一种高效拜占庭容错共识算法 PBFT是Practical Byzantine Fault Tolerance的缩写，意为实用拜占庭容错算法。该算法是Miguel Castro 和Barbara Liskov（2008年图灵奖得主）在1999年提出来的，解决了原始拜占庭容错算法效率不高的问题。 他的核心思想是：对于每一个收到命令的将军，都要去询问其他人，他们收到的命令是什么。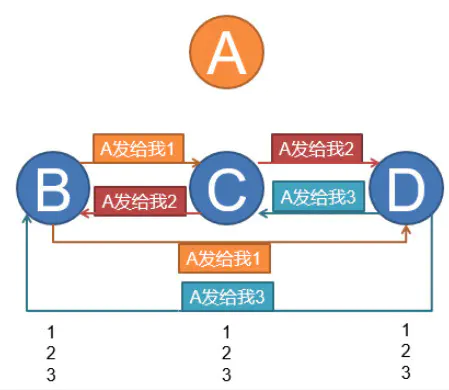 如上图，假设命令由A将军分发，假如A是作恶异常，分发给B,C,D的操作分别是1,2,3.意图扰乱共识。拜占庭容错算法上设计实现是，当B,C,D收到命令后，相互之间也会沟通从A收到的命令是否一致，从而达到识破干扰的目的。其容错的极限值就是N>=3F+1。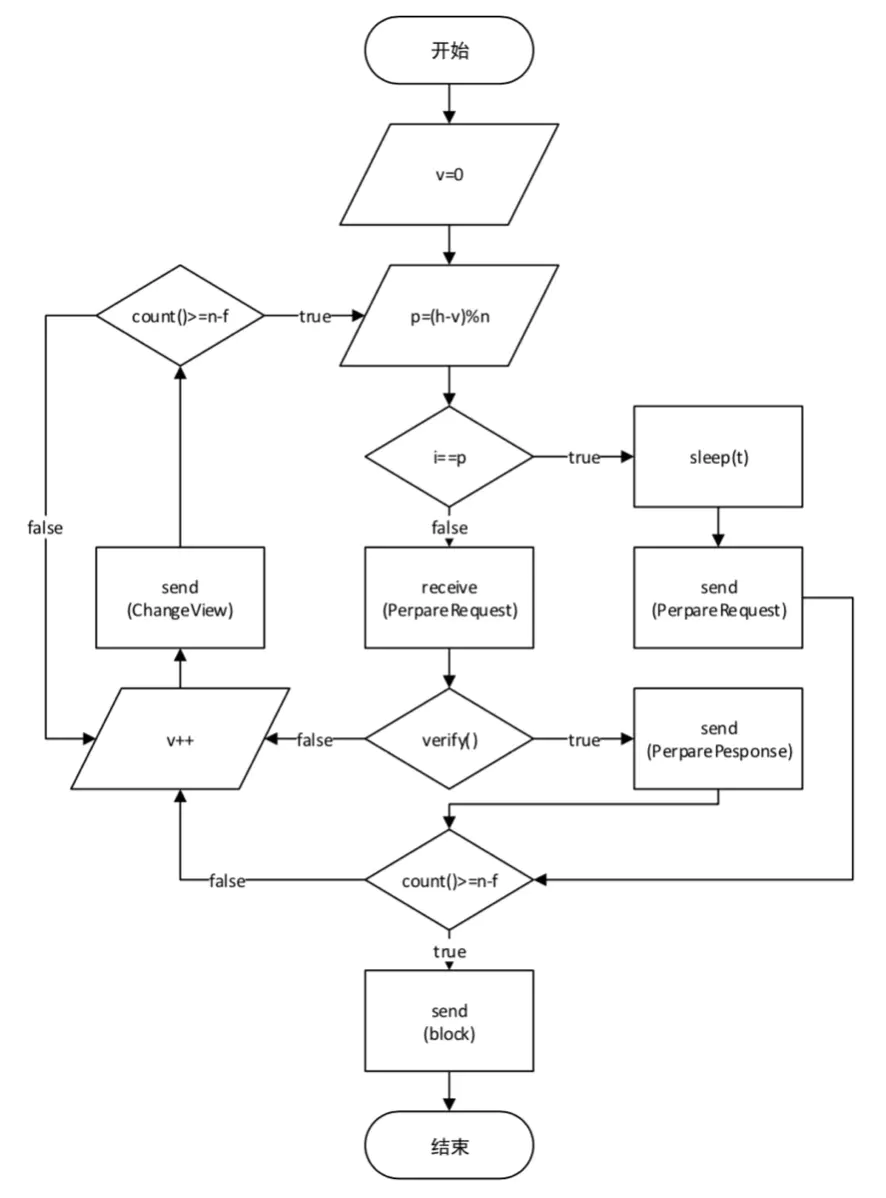 PBFT 在区块链上的实现 区块链的节点分为记账节点和普通节点两个角色 记账节点负责向全网提供记账服务，并维护全局账本，每过一段时间从记账节点中选一个议长，进行命令的分发，其他记账节点则作为议员进行验证 将军就是记账节点，拥有全局账本，并验证交易的有效性，过互相传达验证结果，在f<=(n-1)/3的前提下，可以保证能达到全局的一致性 共识的一般流程如下： 1.任一节点接收到发送者签名的交易数据请求后，向全网广播 2.所有记账节点均独立监听全网的交易数据，并记录在内存 3.议长在经过t后发送共识请求提案request 4.议员在收到提案后，进行相关验证，发送响应response 5.任意节点在限定时间内收到至少F+1个response后，共识达成，把交易记录入区块并发布给全网，如果超时，则更换视图和议长 6.任意节点在收到完整区块后，把包含的交易从内存中删除 开始下一个共识循环 区块产生间隔t, 记账节点n, 可容错节点数f， 视图编号v, 区块高度h, 议长编号p, 议员编号i p=(h-v)%n 未来的发展 POW算法建立了比特币帝国，具有划时代的意义。但其能耗和速度问题却是制约区块链普及的两大难以解决的问题。 目前POS算法是一大趋势，以太坊的Casper，EOS的DPos等都是借鉴了上述前人的设计理念做的基于应用场景的优化改造，但万变不离其宗，我和大家一样，需要不断的学习和思考，没准，能有发明出自己的共识算法的一天呢。